LeetCode Question –
You are given the
rootof a binary search tree and an arrayqueriesof sizenconsisting of positive integers.Find a 2D array
answerof sizenwhereanswer[i] = [mini, maxi]:
miniis the largest value in the tree that is smaller than or equal toqueries[i]. If a such value does not exist, add-1instead.maxiis the smallest value in the tree that is greater than or equal toqueries[i]. If a such value does not exist, add-1instead.Return the array
answer.
Understanding the question –
Let’s understand the question with some simple examples before we proceed with the code. You may skip this section if you already do –
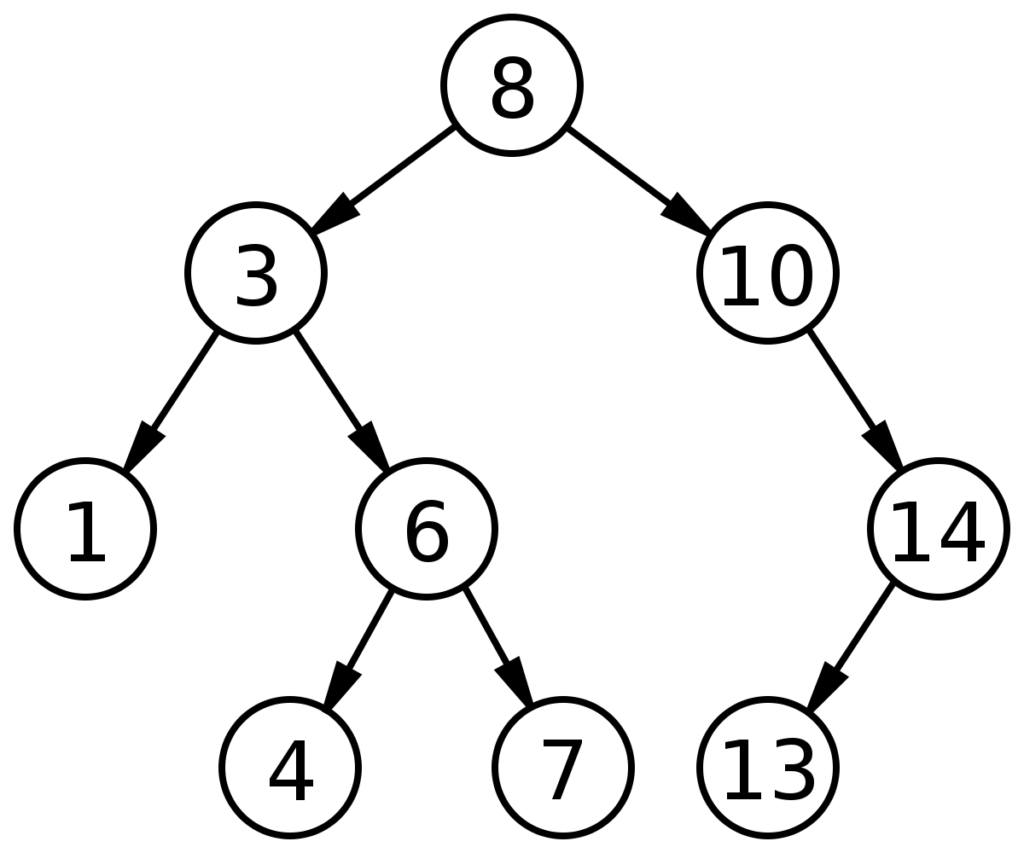
Before we begin, let’s break down the question. The question states that we will be passed a “Binary Tree” and an “answer array“. Let’s assume the “answer array” passed to us to be “[5, 14, 15]” and let us assume the Binary Tree to look like the diagram below.
Find a 2D array
answerof sizenwhereanswer[i] = [mini, maxi]
“i” here refers to the index of the array. Assume that i = 0. The 0th index in our answer array i.e answer[0] = 5. So we need now need to find the “conditional” min and max of 5 from our Binary Tree.
miniis the largest value in the tree that is smaller than or equal toqueries[i]. If a such value does not exist, add-1instead.
“mini” means the minimum number that we can find in our binary tree for our ith index. Let us assume i = 0. The ith index in our answer array is 5. Now minimum here does not refer to the smallest number in the tree lesser than 5. It refers to a number that is equal to 5, or the largest number lesser than 5 in the binary tree.
maxiis the smallest value in the tree that is greater than or equal toqueries[i]. If a such value does not exist, add-1instead.
“maxi” means the maximum number that we can find in our binary tree for our ith index. Let us assume i = 0. The ith index in our answer array is 5. Maximum here does not refer to the greatest number in the tree greater than 5. It refers to a number that is equal to 5, or the smallest number greater than 5 in the binary tree.
Now that we’ve understood the question. Let us move ahead with our approach.
Approach –
We will break down our approach into 3 checks –
- If the tree contains our target number, then we return the target number as our min and max.
- If our target number does not exist, then we will find out all the numbers lesser than and greater than our target number and then find our min and max accordingly.
- If there are no numbers lesser than and/or greater than our target number, then we simply return -1 in either min or max or both.
Example 1 –
For our first example, let us assume that the target number given to us is “5“.
Now let’s go through our checks. First of all, notice that our target number does not exist in our Tree. Given that fact, let us move on to our next check. Let’s first look at all the numbers in our Tree that are lesser than our target number. They are “1“, “3” and “4“. The maximum number here is “4“, so we simply set this number as our min. Next, let’s look at all the numbers greater than our target number. They are “6“, “8“, 10“, “13” and “14“. The minimum number here is “6“, so we simply add this number as our max. As such, we have received our conditional min and max for our target number, them being “4” and “6“.
Example 2 –
For our second example, let us assume that the target number given to us is “14“.
As our target number exists in our Tree, we will simply set both our min and max as “14“.
Example 3 –
For our third example, let us assume that the target number given to us is “15“.
Going through check 1, we notice that our target number does not exist in our Tree. Going through check 2, we notice that all the numbers in our Tree are lesser than our target number, the largest of them being “14“. As such, we set our min as “14“. We however notice that there are no numbers in our Tree that are greater than our target number and as stated in our third check, if there are no numbers that are lesser/greater than our target number, then we simply set our min/max to “-1“. In this case, there are no numbers greater than our target number, so we simply set max to “-1“. As such, we have received our conditional min and max for our target number, them being “14” and “-1“.
To put it in simple words, if the target number exists in our Binary Tree, then we simply return the number as the min and the max. If not, then we return the greatest number that is lesser than the target number and the smallest number that is greater than the target number.
Code –
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> closestNodes(TreeNode root, List<Integer> queries) {
//Initialize the array to be returned
List<List<Integer>> returnedArray = new ArrayList<>();
//Loop through the array of numbers
for(Integer number:queries){
List<Integer> minMaxArray = new ArrayList<>();
//Find the largest and the smallest number based on their criteria
int[] values = this.findMinMax(root, number);
//Store the returned values
Integer min = values[0];
Integer max = values[1];
//Add them to the temporary array
minMaxArray.add(min);
minMaxArray.add(max);
returnedArray.add(minMaxArray);
}
return returnedArray;
}
public int[] findMinMax(TreeNode node, Integer target){
int min = -1;
int max = -1;
//Traverse through the TreeNode Class
while(node != null){
//Return min and max value as the same value if the node value matches the target
if(node.val == target){
return new int[]{target, target};
}else if(node.val > target){
max = node.val;
node = node.left;
}else if(node.val < target){
min = node.val;
node = node.right;
}
}
return new int[]{min, max};
}
}Understanding the code –
In order to understand the code you must know one simple fact about the binary tree and i.e, all numbers lesser than the “parent node” are situated to the left, and all the numbers greater than or equal to are situated to the right. You will understand more about it further down below.
Let us understand the helper method that finds us our min and max, i.e the findMinMax method as the main method simply loops through all the given numbers, finds its min/max and adds it to our end array.
We will break down our approach into 3 checks –
- If the tree contains our target number, then we return the target number as our min and max.
- If our target number does not exist, then we will find out all the numbers lesser than and greater than our target number and then find our min and max accordingly.
- If there are no numbers lesser than and/or greater than our target number, then we simply return -1 in either min or max or both.
We first start by setting both the min and max to “-1”. We do so just in case our Tree does not satisfy both checks 1 and 2, which if it does not, then we can assume that our tree does not contain a min/max for our current number.
We then declare a loop that in the worst case, will run until it has checked all the appropriate nodes till it reaches a dead end i.e till the appropriate node is not null.
In our loop, we go through the above checks.
The first “if” condition satisfies the 1st check, i.e, it checks as to whether the current node contains our target value and if it does, then we simply return that number as our min and max.
The second and third conditions look into multiple conditions that can be understood by an example –

Given the above binary tree, let’s assume that the current number that we’re looking for is “9”.
We start with the root node i.e “8“. This node is lesser than our current number. Our 2nd condition notices that the number is lesser than our current number and sets our “min” to “8“. Now given our knowledge of binary trees, if the node is greater than the current number, then the current number is probably associated to the left, right if not. In this case, since “8” is less than “9“, our current number probably resides on the right side of the parent node. So we switch the node to the right node i.e “10“. We repeat this until we find the current number (1st “if” condition), or a number that is lesser/greater than the current number (2nd and 3rd condition), till we reach a dead end (while loop condition).
Now in this scenario, we end up with the node “10“. This node is greater than our current number. Our 3rd condition notices that the number is greater than our current number and sets our “max” to “10“. It then checks for the next appropriate node. Since node “10” is greater than “9“, we switch to the left node. However, the left node simply does not exist and as such, we can simply assume that our current number does not exist and since we’ve reached a dead end, we break out of the loop. We now have our min and max for the number 9, them being “8” and “10“.
Incase of a number like “15“, our code would go through every appropriate node while setting the number lesser it to min. In this case, following our logic of the code, we end up with the number “14” i.e also a number lesser than “15“. Since “14” is lesser than “15“, we simply assume that the number is to the right of our current node. Since the current node is empty, we simply break through the loop. Now in this case, our min stays set at “-1” since we never traversed/found a number greater than “15” which sets our min and max to “15” and “-1” respectively.
Conclusion
The given statements concludes our problem’s solution. Do feel free to ask any questions regarding the problem if required.
